- Forfatter admin carl@lifeloveeveryday.com.
- Public 2023-12-16 19:25.
- Sist endret 2025-06-01 06:13.

Eksempler på det gylne snitt kan finnes over alt i klassisk arkitektur, kunstverk, natur og til og med musikk. Dette uttrykket av proporsjoner, også kjent som det guddommelige forholdet, tilbyr harmonisk komposisjon gjennom bruk av et irrasjonelt tall (1.618) i design, både naturlig og menneskeskapt. Mest sannsynlig er du ikke klar over regnestykket bak skjønnheten til det gylne snitt fordi det produserer gjenstander og musikk som du naturlig vil finne behagelig uten å trenge noen forklaring.
Golden Ratio in Architecture
The Golden Ratio skaper nesten perfekt skjønnhet i naturen og kunsten. Når du begynner å lete etter Golden Ratio-eksempler i hverdagen, kan du bli overrasket over de mange tilfellene det har blitt brukt til å lage mange monumentale bygninger og strukturer. Når det gylne snitt brukes i arkitektur, sies bygningen å være skapt ved å bruke «hellig arkitektur». Ved å bruke beregningen av det gylne snitt på en firkant, er arkitekter og designere i stand til å lage det gylne rektangel, som antas å ha de mest estetisk tiltalende proporsjonene for det menneskelige øyet.
Gyldent rektangel Eksempel: Parthenon

Phidias, den greske billedhuggeren, brukte det gylne snitt i arbeidet sitt, spesielt da han begynte å jobbe med båndene han skulpturerte like over Parthenonsøylene. Det er også viktig å merke seg at den numeriske verdien som er tildelt det gylne snitt, Phi, ble navngitt til hans ære.
Hvis du måler dimensjonene til Parthenons eksteriør, vil du oppdage at det ikke bare danner et gyldent rektangel, men at det også er mange gylne rektangler mellom søylene. Denne hellige strukturen er et vakkert eksempel på det gylne snitt i arkitektur.
Golden Triangle Eksempel: Great Pyramid of Giza
Det gylne snitt, det gylne rektangelet og det gylne trekantet kan alle bli funnet i perfeksjonen til et av verdens syv underverker, den store pyramiden i Giza. For å finne det gylne snittet, må du halvere den firkantede bunnen av pyramiden og tegne en vertikal linje opp i midten av pyramiden. Når denne er koblet til en vinklet side av pyramiden, kan du enkelt se hvordan den danner Golden Triangle med et forhold på 1,618, Golden Ratio.
Andre arkitektoniske eksempler
Du kan finne mange eksempler på gammel til moderne hellig arkitektur og bygninger med gyldent snitt.
- Chartres Cathedral - Centre, Frankrike
- Notre Dame - Paris, Frankrike
- Porch of Maidens - Akropolis, Athen
- Taj Mahal - Agra, India
- United Nations Building - New York City, New York
Gyldent snitt i kunsteksempler
Du kan finne mange eksempler av malere som brukte det gylne snitt. Disse perfeksjonsverkene ble skapt ved å bruke forholdet mellom gyldne rektangler og gyldne trekanter. Kunst laget basert på det gylne rektangelet viser seg å være mer behagelig for det menneskelige øyet. Det er et av mysteriene som omgir dette perfekte rektangelet og det gylne snittet.
Golden Ratio in Art

Kunsteksempler med gyldne snitt inkluderer:
- Leonardo Di Vinci - Mona Lisa, Vitruvian Man
- Botticelli - Venus fødsel
- Michelangelo - Holy Family, 'David'
- Raphael - Korsfestelse
- Rembrandt - Selvportrett
- Salvador Dali - Nattverdens sakrament, minnets utholdenhet
Using Golden Ratio i kunstkomposisjon
Innenfor et gyldent rektangel er visse områder funnet å være mer visuelt tiltalende enn andre områder. Disse punktene oppdages ved å tegne en linje fra det nederste hjørnet av rektangelet til det motsatte hjørnet og gjenta det med det andre nederste hjørnet. Disse linjene vil krysse i det nøyaktige sentrum av det gylne rektangelet. Deretter måler du midtveis langs hver linje fra midtpunktet. Disse fire punktene kalles øynene til rektangelet (Golden Ratio). Maleriets hovedfokus blir deretter tegnet eller m alt innenfor disse interessepunktene (forhold).
Golden Ratio in Music

Musikk er sammensatt av numerisk verdi, og når det gylne snitt brukes til å lage et musikalsk stykke, blir det et levende eksempel på matematikk. Fibonacci-sekvensen er også utbredt i musikk:
- Det er åtte toner i en skala.
- Tredje- og kvinttonene er grunnlaget for akkorder.
- Lengden, eller oktaven, til en hvilken som helst note er 13 toner.
Sekvenseringen fortsetter gjennom et musikkstykke og blir mer kompleks når det når det gylne snitt.
Komponister som brukte det gylne snitt
Noen av de mest kjente klassiske komponistene brukte Golden Ratio og Fibonacci Sequencing i musikkstykkene sine, inkludert Bach, Beethoven, Chopin og Mozart. Noen moderne komponister som Casey Mongoven har utforsket det gylne snitt i musikken sin.
Golden Ratio-eksempler i naturen

Hvor finnes det gylne snitt i naturen? Det er i Golden eller Fibonacci Spiral, som kan lages ved å bruke Golden Ratio. Dette er et fenomen som finnes mye i den naturlige verden. En plantes blader vokser slik at så mange som mulig kan spiral oppover stilken. Et nytt blad dannes først etter at den som fortsetter det har dannet seg.
- Spiralkaktus
- Spiralgalakser
- Solsikker
Blomster med Fibonacci-sekvensen
Noen blomster har blomsterblader som følger Fibonacci-sekvensen:
- Tre kronblad:Iris, lilje, orkideer, trillium
- Fem kronblad: Smørblomster, pelargonier, hibiscus, morning glory, nasturtium
- Åtte kronblad: Delphiniums
- 13 kronblad: Visse varianter av tusenfryd, ragwort, ringblomst
Fibonacci-spiral i furukongler

Avhengig av treslag kan du også se Golden Ratio i arbeid innenfor en Fibonacci-tallserie i kongler. Du kan finne en serie på åtte spiraler på den ene siden av furukonglen, med 13 spiraler på den andre. Et annet konglemønster har fem spiraler på den ene siden med åtte på den andre.
Golden Ratio in Humans
Dette forholdet er også viktig for ikke bare hvordan mennesker ser på hverandre, men også for hvordan kroppen deres fungerer, og i deres DNA.
DNA avslører det gylne snitt
Et av de mest fantastiske eksemplene på Golden Ratio finnes i den menneskelige DNA-strukturen. Dette kan sees i et enkelt DNA-tverrsnitt som avslører at DNA-dobbelthelixen danner en tikantform. Dette er en kombinasjon av to femkanter, rotert 36 grader fra hverandre, danner DNA-dobbelhelixen. Selve den doble helix-spiralen danner en femkant. Selv et enkelt DNA-molekyl avslører grunnlaget for det gylne snitt eller guddommelig proporsjon.
Matematikken bak det gylne snitt
Å finne det gylne snittet i det virkelige liv er enkelt, slik det ser ut rundt deg. Det er en matematisk truisme som brukes til å definere det som vanligvis er kjent som det perfekte tallet som finnes i naturen som har blitt duplisert og imitert av mennesker i århundrer. Den forenklede skjønnheten til dette nummeret skjuler dets kompleksitet i utførelsen. For å forstå teorien bak det gylne snitt, må du først utforske Fibonacci-sekvenseringen av forholdet.
Fibonacci-sekvensen og det gylne snitt
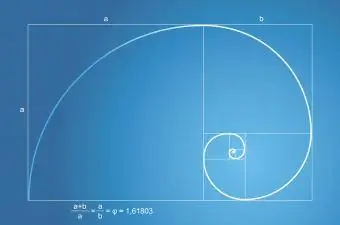
Fibonacci-sekvensen eller -serien har et forhold til Golden Ratio. Fibonacci-serien viser seg i antall blader på en plante og antall kronblader på en blomst. Fibonacci-spiralen, som finnes i naturen, er alltid en del av et gyldent rektangel med et gyldent snitt.
Fibonacci-seriens matematikk er enkel:
- Sekvensen begynner med 0 og 1.
- Bare legg til de to siste tallene for å få det neste tallet i serien.
- 0+1=1, 1+1=2, 1+2=3, 2+3=5, 3+5=8, og så videre.
- Dette Fibonacci-eksemplet blir: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 og så videre.
Fibonaccis forhold til Golden Ratio blir realisert når det legges fremover, lenger og lenger. Jo mer du legger til serien, jo nærmere det gylne snitt kommer du.
Lage et gyldent rektangel og trekant
For å lage et gyldent rektangel med Fibonacci-sekvensen, starter du med en firkant. Du vil begynne å bygge et rektangel ved å legge til en annen firkant til den opprinnelige firkanten. Husk å bruke formelen: 0+1=1 er det første kvadratet, 1+1=2 - du legger til et annet kvadrat.1+2=3 legger du til tre ruter og deretter, 2+3=5, legger du til fem ruter. Du vil fortsette å legge til firkanter og til slutt danne et gyldent rektangel.
En gylden trekant kan lages ved å halvere et gyldent rektangel fra det ene hjørnet til det motsatte hjørnet. Dette skaper en trekant der de tre sidene eller vinklene har et forhold på 2:2:1, noe som betyr at de to lange sidene er like lange og den korte vinkelen er nøyaktig halvparten av lengden av de to lengre.
Golden Ratio in the Real World
Det gylne snitt blir ofte referert til som det guddommelige forholdet på grunn av dets fremtredende plass i naturen og i menneskekropper. Oppdagelsen av at det gylne snitt er tilstede i så mange levende ting fremmet en ærbødighet for denne magiske andelen, og den fortsetter å være en inspirasjon for kunstnere og skapere i dag.






